BELLMAN FORD's ALGORITHM

Bellman Ford's Algorithm - Single Source Sortest Path - Directed Graphs

Bellman Ford's Algorithm is almost same as Dijkstra's Algorithm. The only advantage of Bellman Ford's Algorithm is it can calculate the Shortest Path even if an Edge has a negative weight.

Note : You do not need to know Dijkstra's Algorithm to know Bellman Ford's Algorithm. We will explain Bellman Ford's Algorithm from scratch.

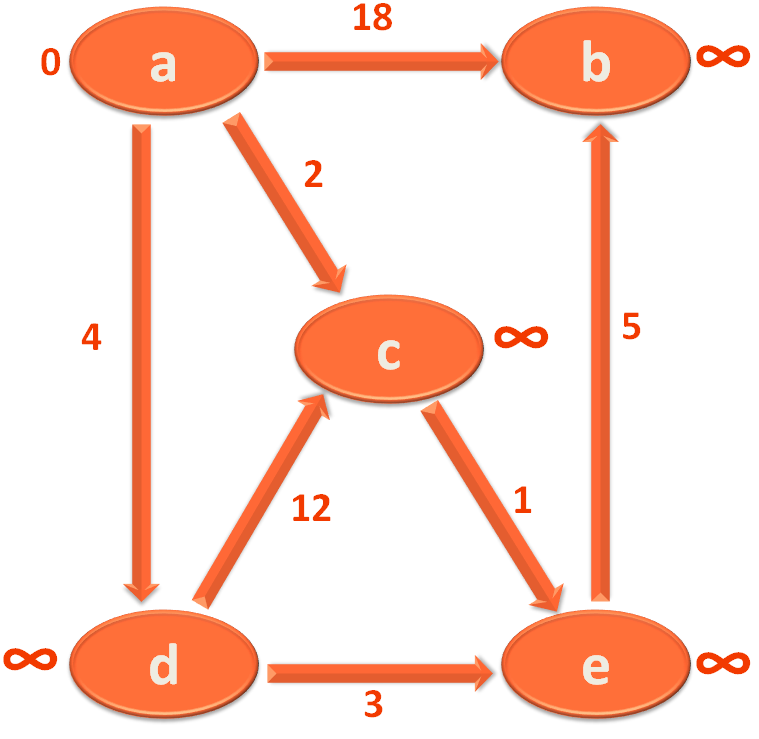
To understand Bellman Ford's Algorithm for Single Source Sortest Path, we will be using the below directed Graph.

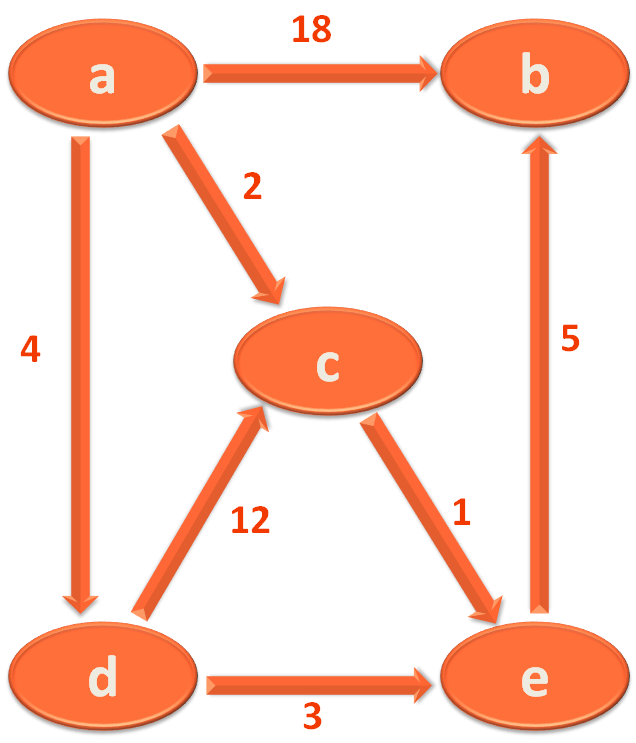
Let us understand Bellman Ford's Algorithm for Single Source Sortest Path, with the example we were using so far.

Example :

We have supposed a, b, c, d and e are the Cities from the above Graph and the Edges are the roads connecting them.

i.e. City 'a' and 'b' is connected by the Road/Edge a,b with length/weight 18. In simple words, let's say, the road connecting City 'a' and 'b' is 18 KMs.

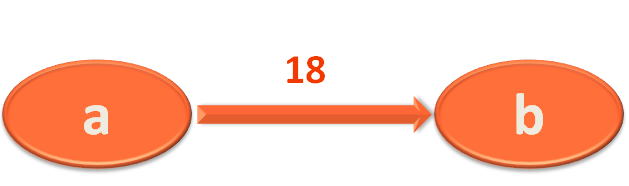
And it is a one way road. i.e. Using this road, you can travel from City 'a' to 'b' but you cannot come back from City 'b' to 'a'.

And the same applies for all the Roads/Edges.

Quite Simple ! Right !

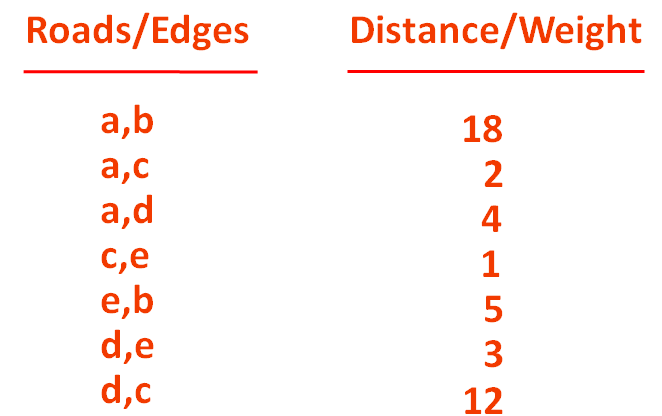
So, let us list out all the Roads/Edges and their distances/weights connecting the Cities/Vertices.

Now, just like the previous examples, you are the delivery guy in a courier company. Due to your good work you were doing so far. Your Manager had given you a Promotion.

Now, you are the region head.

And this time your Manager has given you a new role. i.e. To find out the sortest distance between the source City to all other Cities.

Let us suppose, the Source City is 'a' in this case.

In simple words, just imagine ! What is the shortest distance between City/Vertex 'a' to City/Vertex 'b'?

Is shortest distance between City/Vertex 'a' to City/Vertex 'b', 18 KMs?

But there is an alternate way to reach City 'b' from City 'a'.

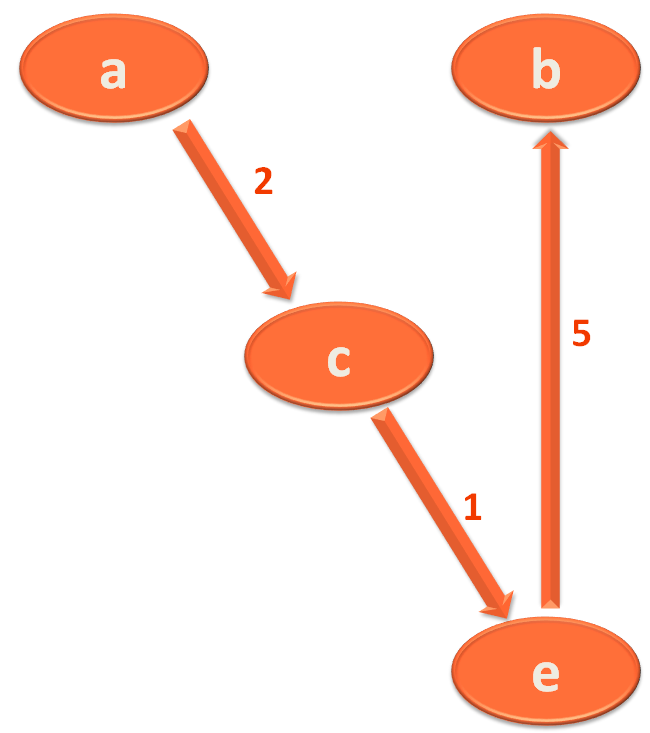
i.e. You travel from City/Vertex 'a' to 'c' first then you can travel to City/Vertex 'e' from 'c'. And finally, you reach the City/Vertex 'b' from 'e'.

So, the alternate path from City/Vertex 'a' to 'b' is :

Now, if we add up the Distances/Weights of the above Roads/Edges.

2 + 1 + 5 = 8

So, if we follow the path a,c,e,b the total distance travelled would be 8 KMs.

But if you travel from 'a' to 'b' your travelling distance would be 18 KMs, which is a lot more.

And in the same way you have to figure out all possible ways and find out the shortest distance between the source City/Vertex 'a' to all other Cities/Vertices :

a --> b
a --> c
a --> d
a --> e

But, why this idea, to find the shortest distance between Cities/Vertices ?

Because it would save the fuel cost for the Vehicles used to deliver Courier packages.

Fair enough !

Now, you are intelligent enough to guess that the Shortest distance between the Source City/Vertex and all the other Cities/Vertices could be calculated using Bellman Ford's Algorithm for Single Source Sortest Path.

So, you will use the 'mark' and 'relax' approach.

And what is that ?

Say you need to find the shortest path between City/Vertex 'a' to City/Vertex 'b'.

If you see the Graph,

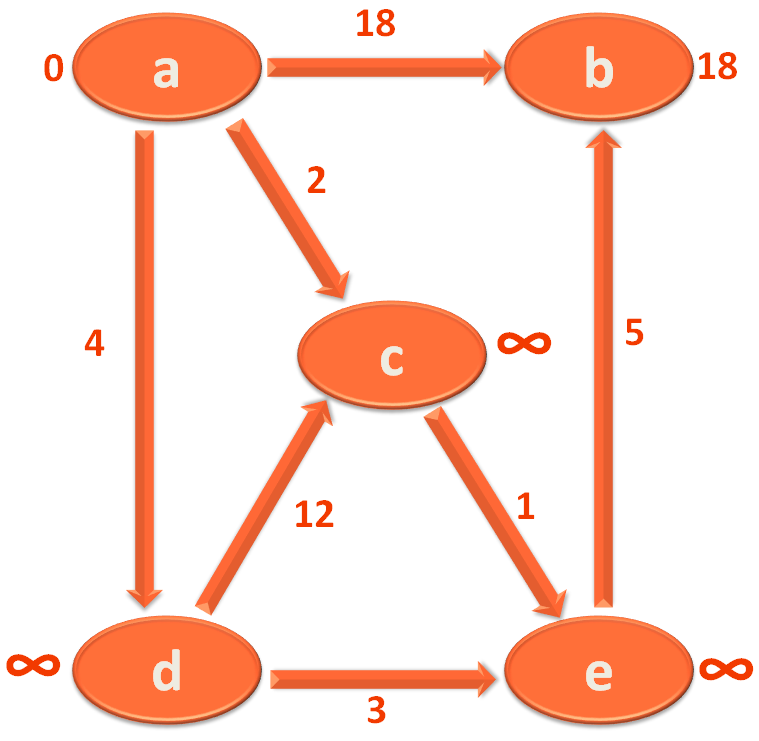
There is a straight route from 'a' to 'b' with distance/weight 18.

And this is where you follow the 'marking' approach.

You simply mark the starting City/Vertex 'a' with '0'(As 'a' is the starting city/vertex and you have to travel 0 KMs to come to 'a') and then mark the City/Vertex 'b' with the travelling distance i.e. 18(Because you have to travel 18 KMs to reach 'b' from 'a').

And then you find, there is one more route through which you could reach 'b' from 'a'.

i.e. You travel from 'a' to 'd' first then travel from 'd' to 'e' and finally from 'e' to 'b'.

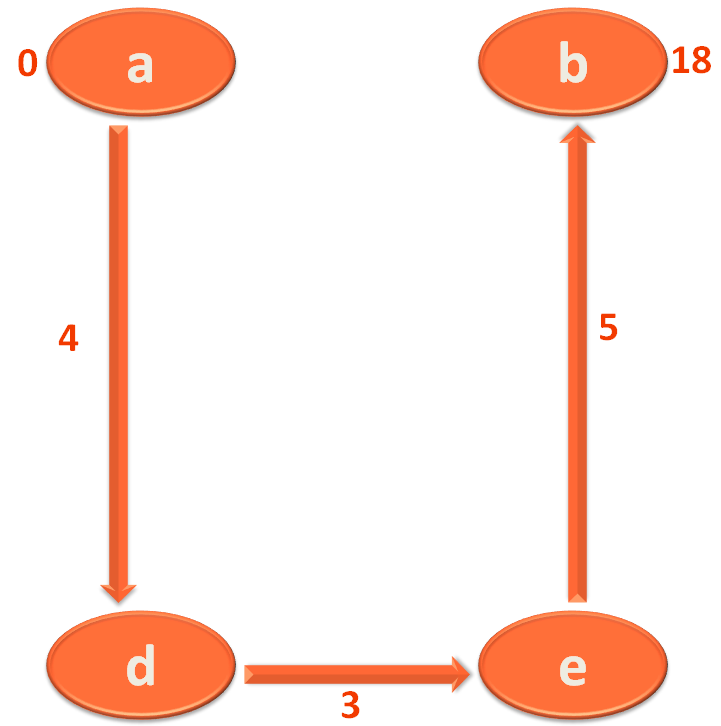
Even here, you follow the same 'marking' strategy.

And as we know the City/Vertex 'a' is already marked with '0' and 'b' is marked with '18'.

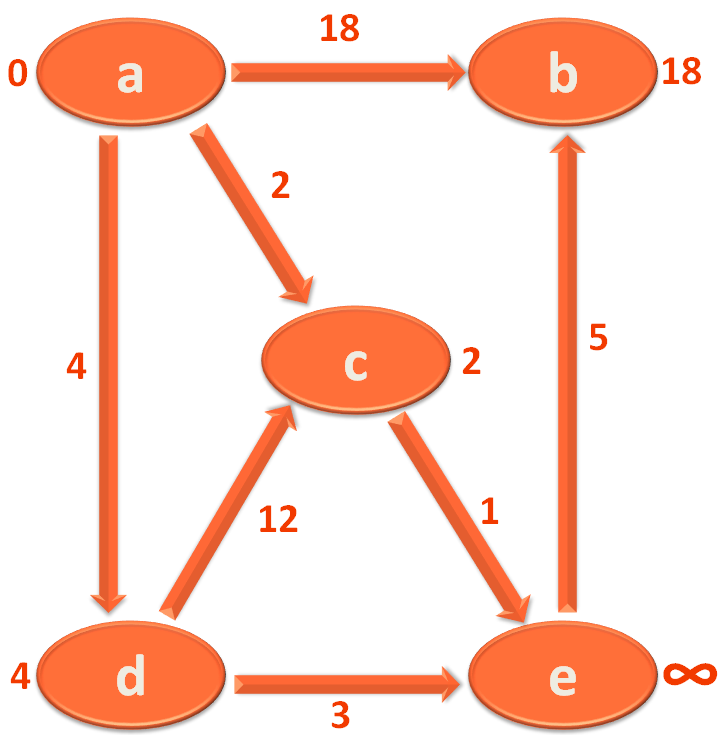
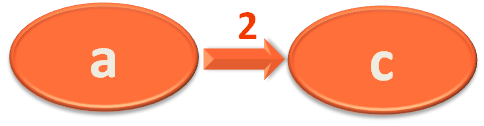
Now, at first when you travel from City/Vertex 'a' to 'd'. You find the distance between 'a' to 'd' is 4 KMs.

So, you mark City/Vertex 'd' with 4. Which actually means you have travelled 4 KMs to reach 'd' from 'a'.

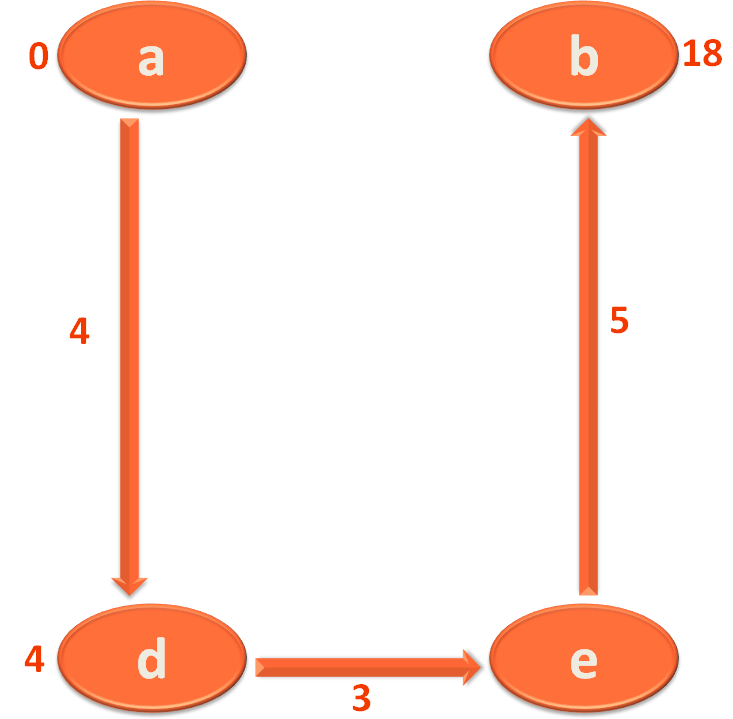
Next, you have to travel from City/Vertex 'd' to 'e'. And you find the distance between 'd' to 'e' is 3.

Now, comes the fun part.

You have already travelled 4 KMs to reach 'd' from 'a'. Now, you have to travel 3 more KMs to reach 'e' from 'd'.

So, the total distance from City/Vertex 'a' to 'e' would be

4 + 3 = 7

i.e. The value of 'd' which is 4 and the distance between 'd' to 'e' which is 3.

And thus, you mark City/Vertex 'e' with this value 7.

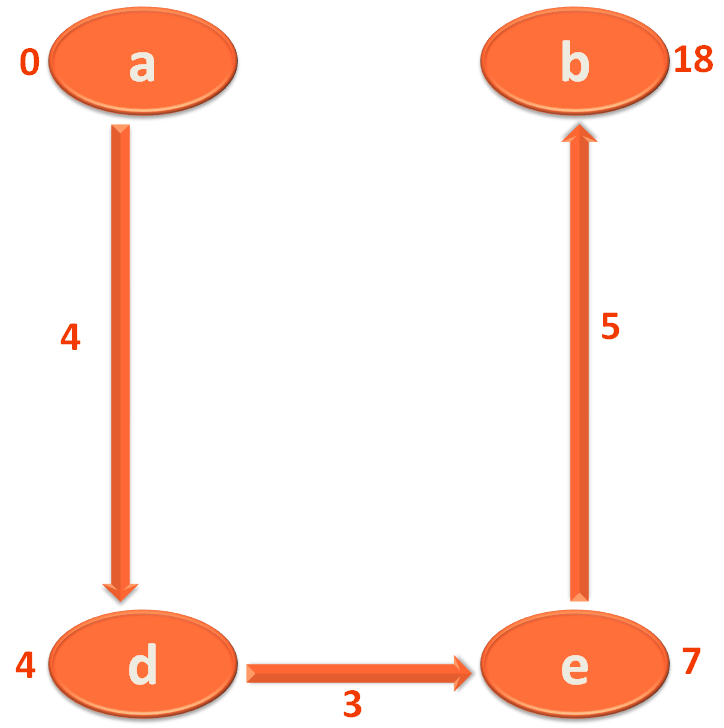
And finally, to travel from City/Vertex 'e' to 'b' you have to travel 5 more KMs.

So, you check, what is the value that is marked with City/Vertex 'e'?

You find that it is 7.

And the distance between City/Vertex 'e' to 'b' is 5.

So, the new total distance from City/Vertex 'a' to 'b' would be,

7 + 5 = 12

And the interesting thing you find is, the new distance from City/Vertex 'a' to 'b' is 12.

But City/Vertex 'b' is marked with 18. Which is more.

So, you came to the conclusion that the direct path between City/Vertex 'a' to 'b' is 18 is more.

Than the new path you found recently, which is 12.

So, what you do is replace/relax the value of City/Vertex 'b' with 12.

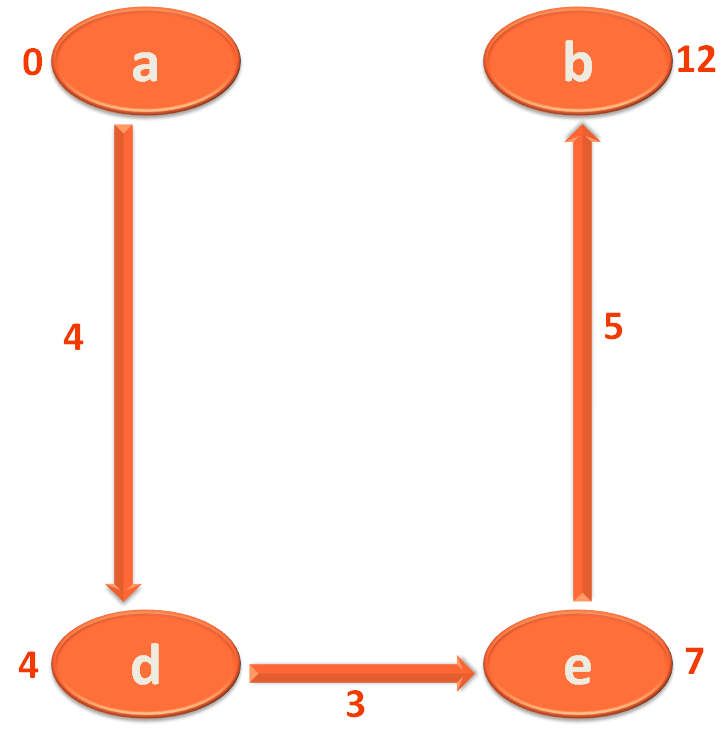
Did I just say replace or 'relax'?

Yes, I did ! The term 'relaxing' is used when you get a smaller path and replace it with the value associated with a City/Vertex.

As we just did. Replaced/Relaxed the value of City/Vertex 'b' with 12.

So, we will be following this process of 'mark' and 'relax' to calculate the Shortest Path using Bellman Ford's Algorithm.

Now, the million dollar question is, how many times do you need to perform this 'mark' and 'relax' process?

Well ! The answer is 'mark' and 'relax' process has to be continued exactly 'V - 1' times. Where 'V' is the number of Vertices/Cities.

And why is that ?

Because if there are 5 Vertices/Cities in a Graph. At max you need to travel through 4 Edges/Roads to reach from starting vertex to ending vertex.

Calculation of Single Source Sortest Path using Bellman Ford's Algorithm

The first thing you will do is, mark all the Cities/Vertices with '∞' except the starting city/vertex 'a'. As 'a' should be marked with '0'.

But why '∞'?

Because we are suppose to find the smallest path. And '∞' can be considered as a very large value, that is not yet assigned.

Let us suppose, you have started from Vertex/City 'a'. So, you would be marking 'a' with '0' and rest of the Vertices/Cities with '∞'.
The next thing you would do is, list out all the Roads/Edges and their Distance/Weight.

So, we got all the Edges/Roads. Now, it is time for us to start relaxing them.

Confused ?

Let us simplify it by seeing the actual process.
The first Edge/Road in our list is a,b with Distance/Weight 18.

Now, since the City/Vertex 'b' is marked with infinity. It can be replaced/relaxed with the new Distance/Weight 18. As the new Distance/Weight i.e. 18 is smaller than '∞'.
Similarly, we will take the second and third Roads/Edges i.e. a,c with Distance/Weight 2 and a,d with Distance/Weight 4.

And replace/relax the value of City/Vertex 'c' with 2(As the new Distance/Weight i.e. 2 is smaller than '∞'). And replace/relax the value of City/Vertex 'd' with 4.
Then we take the fourth Edge/Road from our list i.e. c,e with Distance/Weight 1. And check the current value of City/Vertex 'c'.

We find the current value City/Vertex 'c' is 2. In other words you have travelled 2 KMs from City/Vertex 'a' to reach City/Vertex 'c'.

Now, you need to travel from City/Vertex 'c' to City/Vertex 'e'. And the total distance from 'a' to 'e' would be,

2 + 1 = 3

So, you need to travel a total distance of 3 KMs to travel from 'a' to 'e'. And you replace/relax the City/Vertex 'e' with 3(As the new Distance/Weight i.e. 3 is smaller than '∞').
Similarly, you take the fifth Edge/Road from our list i.e. e,b with Distance/Weight 5. And check the current value of City/Vertex 'e'.

We find the current value City/Vertex 'e' is 3. In other words you have travelled a total distance of 3 KMs from City/Vertex 'a' to reach City/Vertex 'e'.

Now, you need to travel from City/Vertex 'e' to City/Vertex 'b'. And the total distance from 'a' to 'b' would be,

3 + 5 = 8

So, you need to travel a total distance of 8 KMs to travel from 'a' to 'b'. And you replace/relax the City/Vertex 'e' with the new value 8(As the new Distance/Weight i.e. 8 is smaller than '18').
Next, you take the sixth Edge/Road from our list i.e. d,e with Distance/Weight 3. And check the current value of City/Vertex 'd'.

We find the current value of City/Vertex 'd' is 4.

Now, you need to travel from City/Vertex 'd' to City/Vertex 'e'. And the total distance from 'a' to 'e' would be,

3 + 5 = 8

Now, if you check the value associated with City/Vertex 'e'. It is 3, which is a lot lower than 8.

So we do not replace/relax the value associated with City/Vertex 'e' with 8. And rather keep it 3.
And finally, we take the seventh Edge/Road from our list i.e. d,c with Distance/Weight 12. And check the current value of City/Vertex 'd'.

We find the current value of City/Vertex 'd' is 4.

Now, you need to travel from City/Vertex 'd' to City/Vertex 'c'. And the total distance from 'a' to 'c' would be,

4 + 12 = 16

Now, if you check the value associated with City/Vertex 'c'. It is 2, which is a lot lower than 16.

So we do not replace/relax the value associated with City/Vertex 'c' with 16. And rather keep it 2.

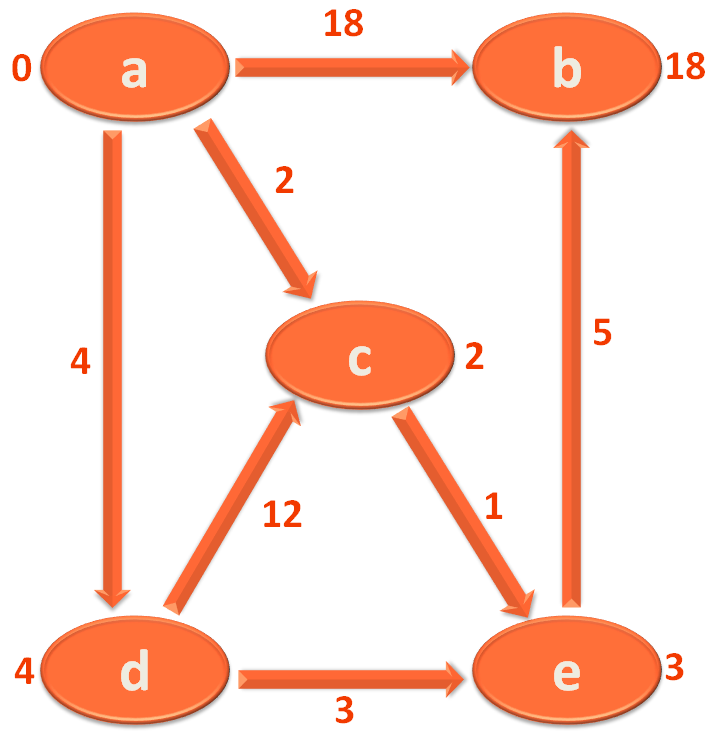
So, we have completed the 1st Iteration. Now, it is time to start the second iteration and continue 'V-1' times.

Where V is the number of Vertices.

In this case there are 5 Vertices/Cities. So, you need to have 4 iteration in total.

So, we start the same process again.

As usual we will, list out all the Roads/Edges and their Distance/Weight.

And start relaxing them.
The first Edge/Road in our list is a,b with Distance/Weight 18.

Now, since the City/Vertex 'b' is already marked with 18. We do not replace/relax the value of 'b'.
Then we deal with the second Road/Edge i.e. a,c with Distance/Weight 2. And find that 'c' is already marked with 2. So we do not replace/relax the value of 'c'.
After that we take the third Edge/Road in our list is a,d with Distance/Weight 4. And even in this case we do not replace/relax the value of 'd' as it is already marked with 4.
Then we take the fourth Edge/Road in our list is c,e with Distance/Weight 1. So, we check the value of 'c' i.e. 2 and add 2 with the Distance/Weight of c,e i.e. 1.

2 + 1 = 3

And find that 'e' is already marked with 3.

So, we do not replace/relax the value of 'e'.
Next, we take the fifth Edge/Road in our list is e,b with Distance/Weight 5.

Even in this case we do not replace/relax the value of 'b'. As the current value of 'b' is 8.
Then we take the sixth Edge/Road in our list is d,e with Distance/Weight 3.

There would be no change here as well.
Then we take the seventh Edge/Road in our list is d,c with Distance/Weight 12.

No change here as well.

So, in the same way if we continue Iterating 4 times. There would be no change in this Graph as well. But there are certain Graphs that changes even in 4th Iteration.

So, you have to continue the Iterations 4 times.

The end result we get is,

The value marked at each Vertex/City is its shortest distance from the source Vertex/City 'a'.

The shortest distance from a --> a is 0 KM.
Similarly, the shortest distance from a --> b is 8 KM. As Vertex/City 'b' is marked with 8.

And the shortest path to travel from a to b is,

2 + 1 + 5 = 8
Next, the shortest distance from a --> c is 2 KM. As Vertex/City 'c' is marked with 2.

And the shortest path to travel from a to c is,
Similarly, the shortest distance from a --> d is 4 KM. As Vertex/City 'd' is marked with 4.
And the shortest path to travel from a to d is,
The same way, the shortest distance from a --> e is 3 KM. As Vertex/City 'e' is marked with 3.

And the shortest path to travel from a to e is,

2 + 1 = 3

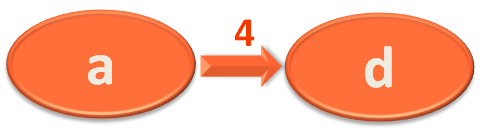
So, you got the shortest distance for all the Vertices/Cities from the source Vertex/City i.e. 'a'.

Now, as said, Bellman Ford's Algorithm for Single Source Sortest Path works perfectly for calculating the shortest distance even if there are negative Edges.

But if a negative edge is present, where the Graph forms a cycle then the Path reduces and the Shortest distance gets reduced at every iteration.

And Bellman Ford's Algorithm has a way to handle it.

How does Bellman Ford's Algorithm handle the problem of negative edges forming a cycle?

As we know, we have to continue the Iteration exactly 'V-1' times to get the Shortest Path. Where V is the number of Vertices.

So, if there are 5 vertices. The iteration should continue 4 times to get the Shortest Path.

And if after iterating 4 times, in the 5th iteration the value reduces then there is a negative Edge in a cycle.

Let us clear with the below Example :

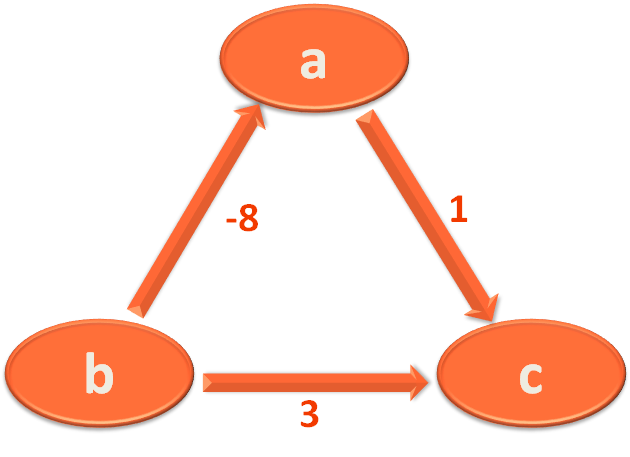
There are three Vertices a, b and c.

And there are three Edges

a --> c - 1
c --> b - 3
b --> a - (-8)

So, we have to iterate (V-1) times

i.e.

3 - 1 = 2 times

So, initially we mark the starting Vertex 'a' with 0 and 'b' and 'c' with '∞'.

1st iteration

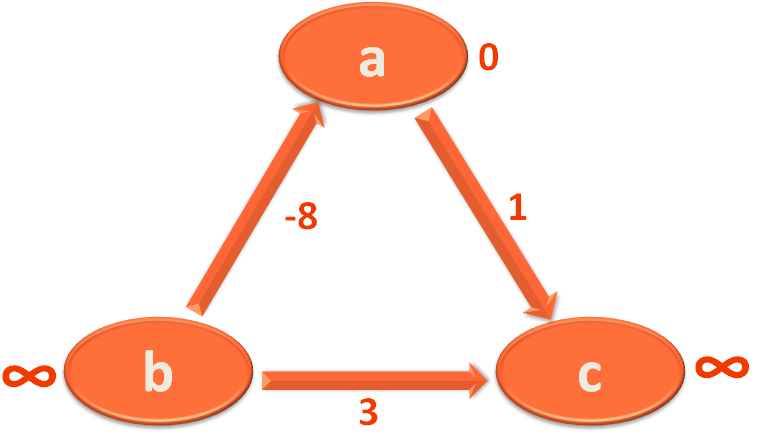
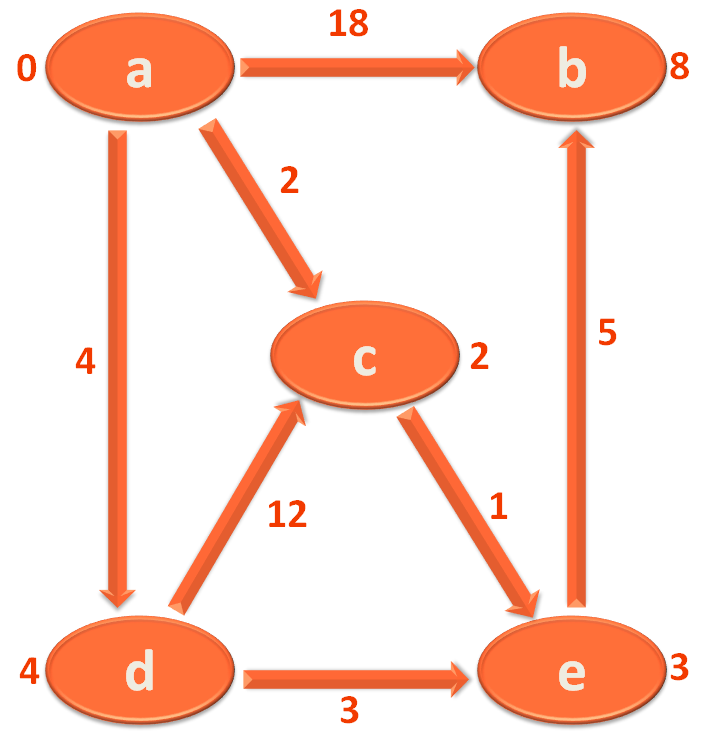
Now, we take the Edge a,c and mark 'c' with 1.

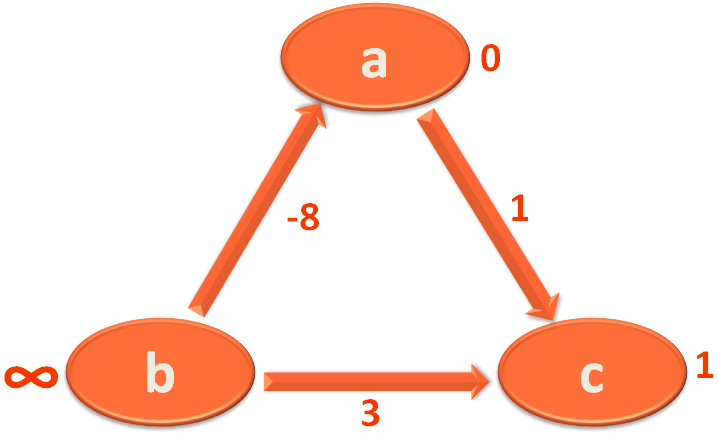
Then we take the Edge c,b and mark 'b' with 1+3=4.

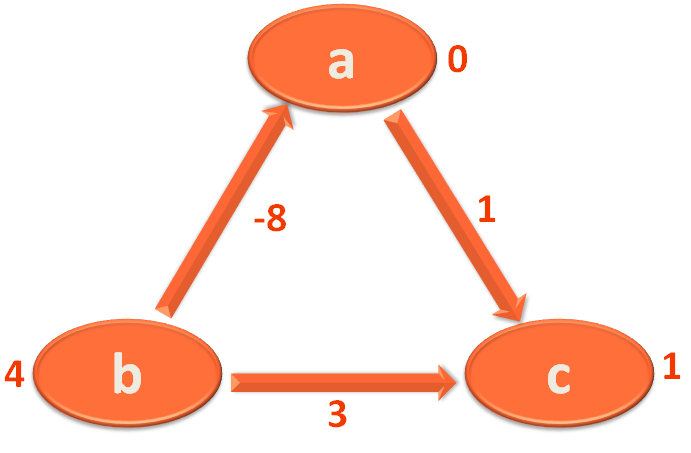
Then we take the Edge b,a and mark 'a' with 4+(-8)=-4.

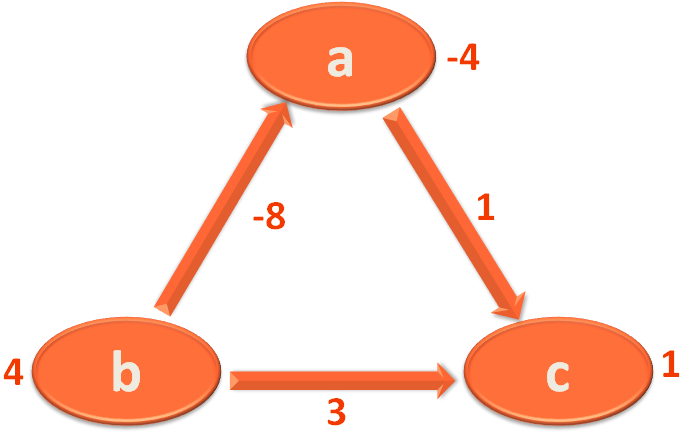
Now, since we are done with all the three Edges, we can proceed with the 2nd Iteration.

2nd iteration

Again we take the Edge a,c and mark 'c' with (-4)+1 = -3.

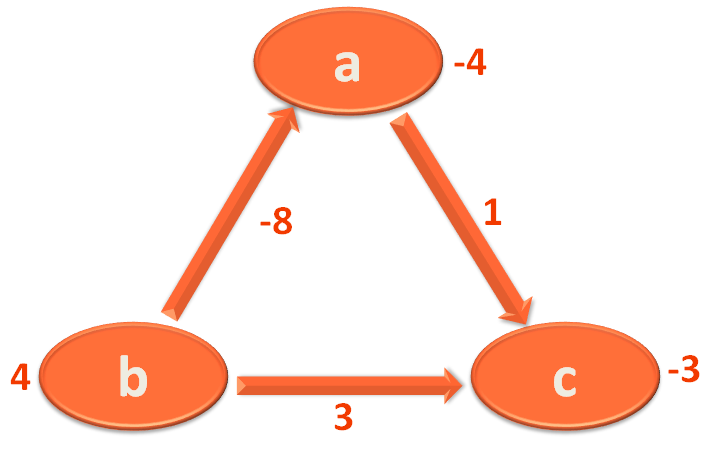
Then we take the Edge c,b and mark 'b' with (-3)+3=0.

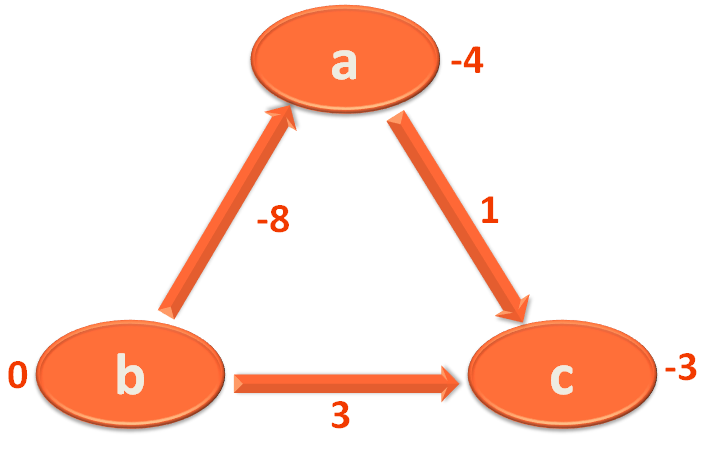
Then we take the Edge b,a and mark 'a' with 0+(-8)=-8.

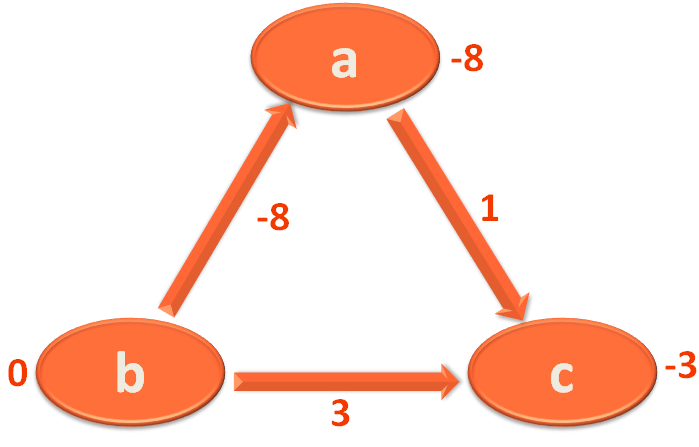
Now, we perform one more Iteration to determine if there is a negative weight cycle.

3rd iteration

Again we take the Edge a,c and mark 'c' with (-8)+1 = -7.

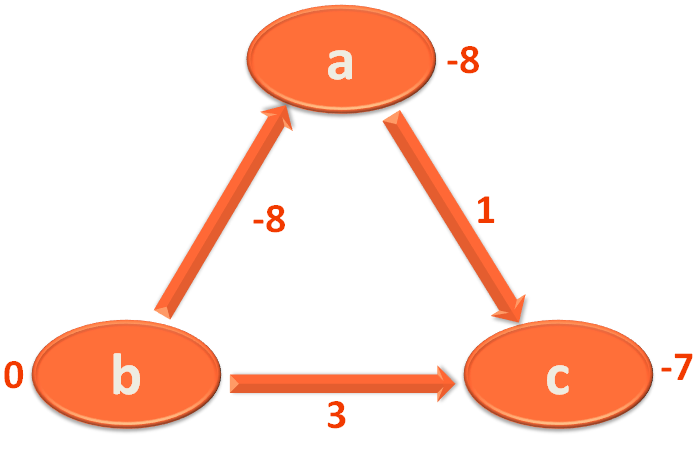
Then we take the Edge c,b and mark 'b' with (-7)+3=-4.

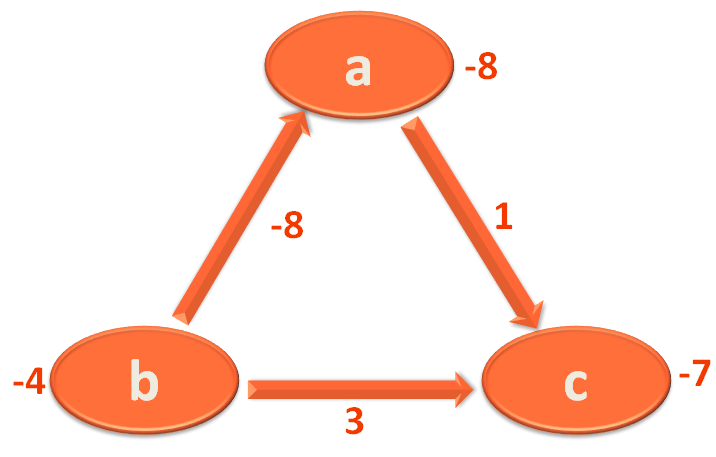
Then we take the Edge b,a and mark 'a' with (-4)+(-8)=-12.

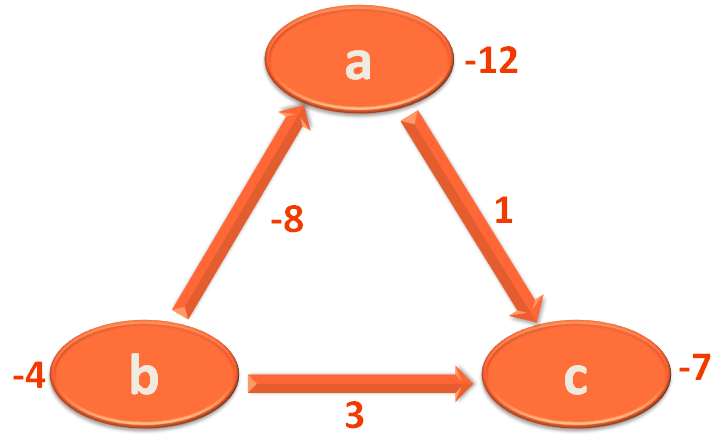
The value of the Vertices are reducing even in the 3rd Iteration. So there is a negative weight cycle present.

❮❮ PREV NEXT ❯❯